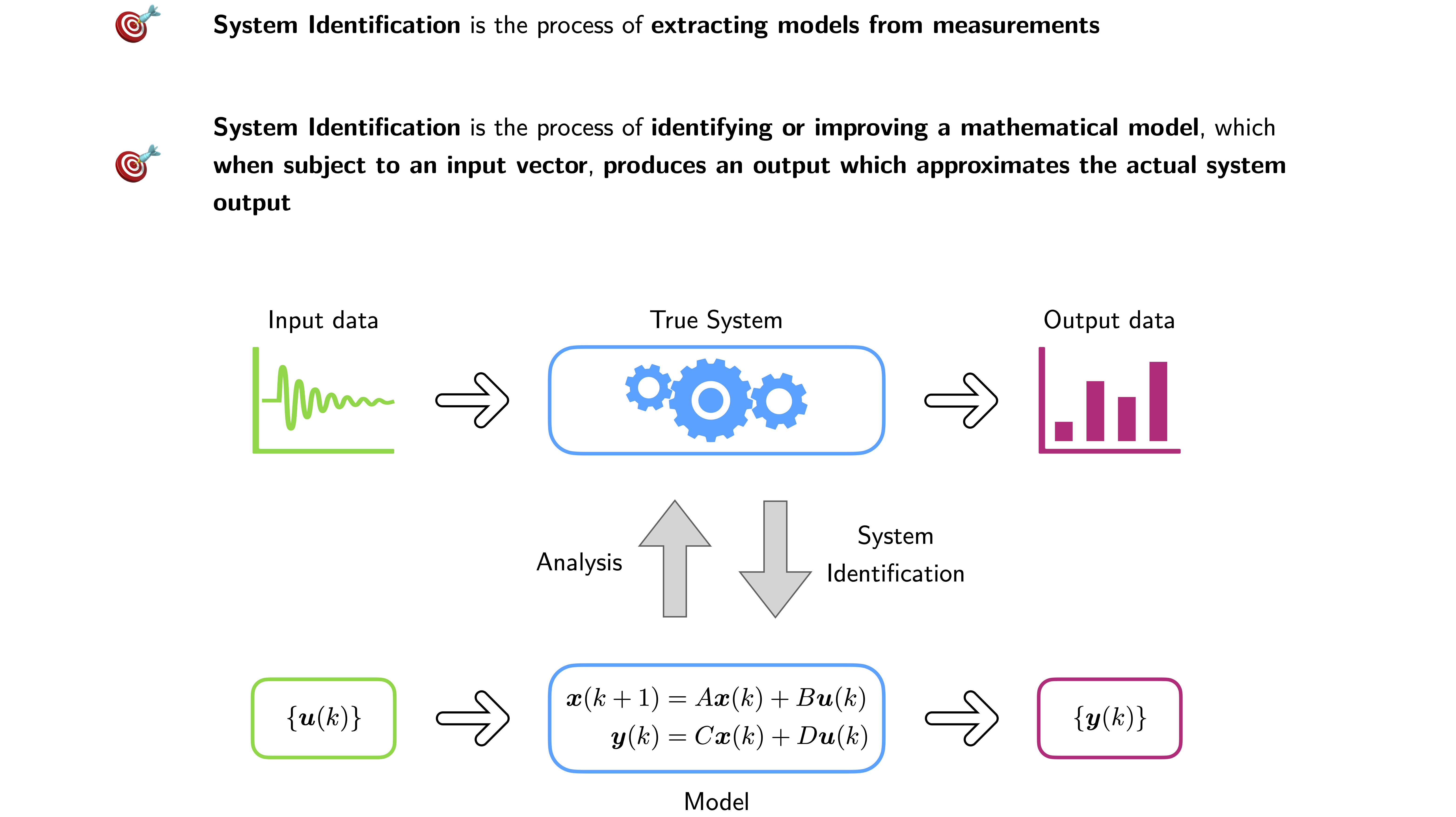
System identification as a research topic has attracted a lot of interest over the last decades and has been an important discipline within the automatic control area, robotics, structural engineering, reduced order modeling and model testing. The special purpose of dynamic system identification corresponds to identifying a mathematical model describing a relationship between input and output of a real system. Recent developments in the field of system identification have provide effective and accurate analytical tools to solve challenging problems in system engineering and virtually in any application concerning models of dynamic systems.

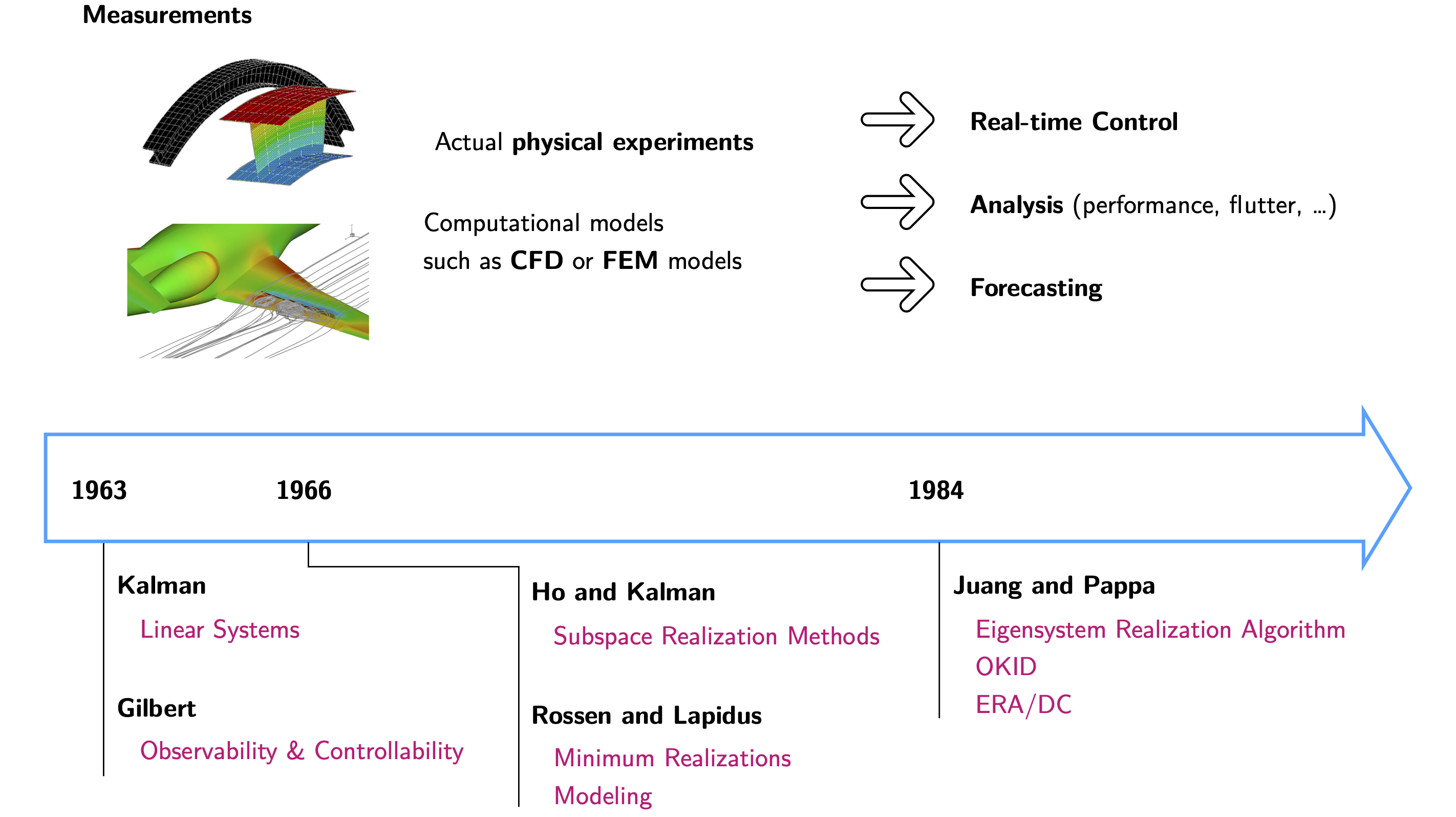
Earlier efforts have been concentrated on linear system identification with a special emphasis on identifying the minimal state space representation to define the subspace over which system dynamics evolves. State-space models are particularly suitable since they lend themselves to linear algebra techniques, robust numerical simulation, and modern control design methods. Among the first were the works of Gilbert and Kalman, which introduced the important principles of realization theory in terms of the concepts of controllability and observability. They first introduced the concept of state-variable equations which realize the external description via an equivalent internal description of a dynamical system. Whether the analyst or the engineer is interested in the synthesis or the analysis, these equations are an efficient and useful model with which one can proceed to further analysis and optimization.

The problem of realization for linear time invariant systems was first stated by Gilbert who gave an algorithm for computing the map transfer function matrix to state-variable differential equations. A second algorithm for the same problem was given at the same time by Kalman using the theory of controllability and observability and requiring linear algebra type computation. A few years later, Ho and Kalman approached this problem from a new viewpoint. They showed that the minimum realization problem is equivalent to a representation problem involving a sequence of real matrices known as Markov parameters (pulse response samples). Minimum realization means a model with the smallest state-space dimension among all possible systems realized that have the same input-output relations and although several techniques of minimum realization are available in the literature, formal direct application to modal parameter identification for flexible structures was not addressed until 1984.

Many algorithms have been established, some of them deterministic in nature, i.e. without considering noise in the measured data, and others stochastic, i.e. with formulations minimizing the noise uncertainty in the identification. During the 90s, building upon initial work by Gilbert and Kalman, several methods has been developed to identify most observable and controllable subspace of the system from given input-output (I/O) data. Under the interaction of structure and control disciplines, the Eigensystem Realization Algorithm (ERA) was developed for modal parameter identification and model reduction of dynamic systems using test data. The algorithm presents a unified framework for modal parameter identification based on the Markov parameters (i.e., pulse response) making it possible to construct a Hankel matrix as the basis for the realization of a discrete-time state-space model.

A few years later at NASA, Juang developed a method for simultaneously identify a linear state-space model and the associated Kalman filter from noisy input-output measurements. Known as the Observer/Kalman Identification Algorithm (OKID) and formulated entirely in the time-domain, it computes the Markov parameters of a linear system, from which the state-space model and a corresponding observer are determined simultaneously. The method relies on an observer equation to compress the dynamics of the system and efficiently estimate the associated system parameters (Markov parameters). In conjunction with the ERA, the method provides simultaneously both the Markov parameters and the Kalman gain, extracting all the possible information present in the data. The observer at the core of the method was proven to be the steady-state Kalman filter corresponding to the system to be identified. Later, the ERA with Data Correlation (ERA/DC) is developed and while the ERA is, in essence, a least-squares fit to the pulse response measurements, the ERA/DC involves a fit to the output auto-correlation and cross-correlations over a defined number of lag values.

This website presents the fundamentals of linear time-invariant system identification and provides a common basis, definitions and notations to understand the techniques developed under the vast discipline of system identification. From discrete-time state-space models, controllability and observability to the famous OKID/ERA procedure, this website introduces the basic building blocks that will be used throughout this dissertation.