Who We Are
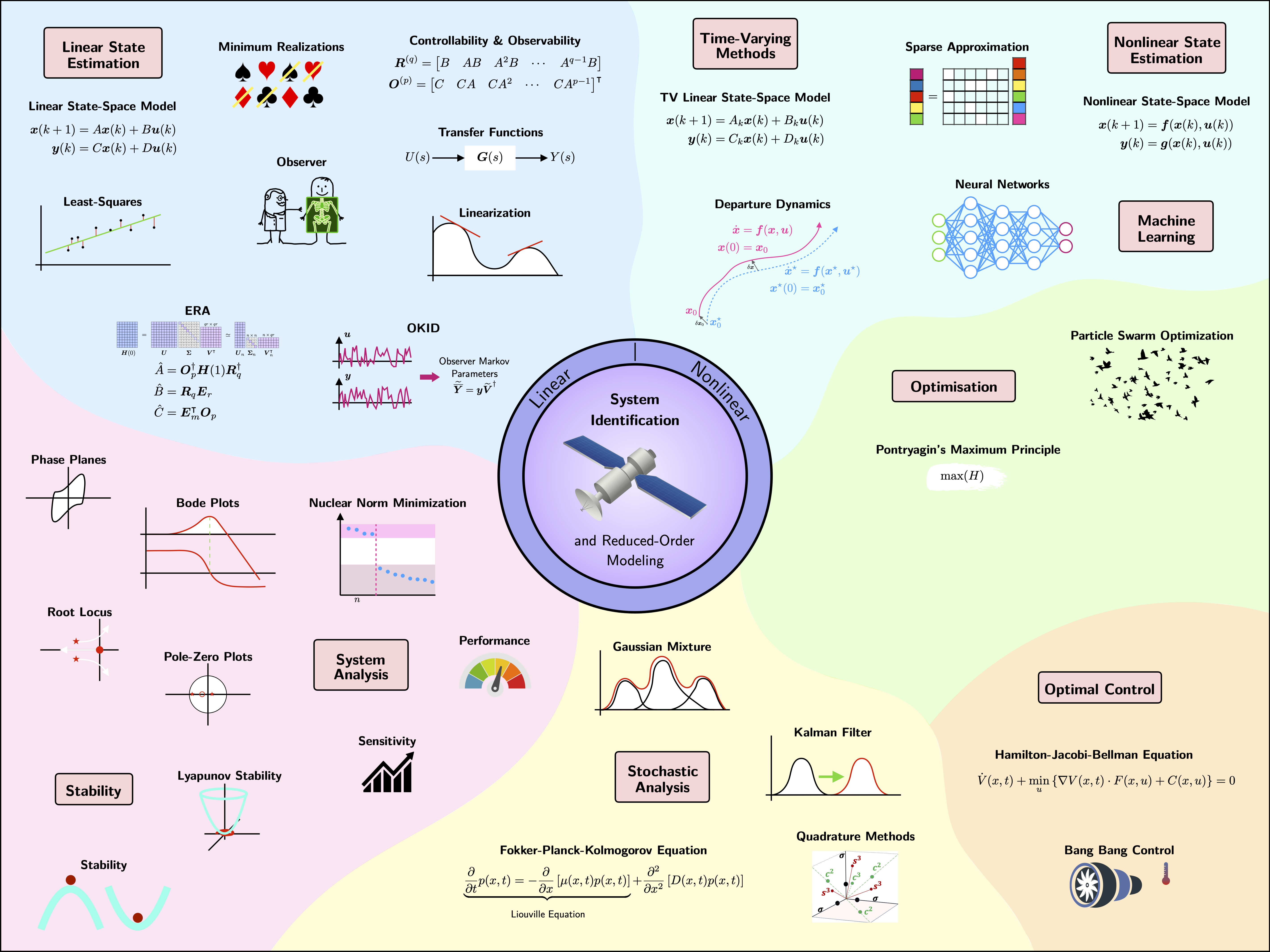
Our Lab is focused on consolidating the complex field of system identification by combining popular linear identification methods (time invariant or time-varying) with newly developed nonlinear sparse identification techniques. The idea is to develop a computationally tractable, robust and dynamic data-driven framework for system identification and reduced-order modeling while addressing challenges associated with accurate modeling, forecasting and control of engineering systems under uncertainty.

Download Contents
All of our supporting documents are publicly available. Check them out and download what you need for your research or classes. Don't hesitate to give us your feedback!
Certain Analysis
We can guide in providing you with the latest techniques and methodologies to apply system identification to your real-life experiments. Contact us to learn how we can help.
Python Source Code
Python source code is publicly available on GitHub. Check it out! Any comment is welcome. And we would love to know how you used our tools to solve some challenging problems.
The research we are conducting in the field of system identification is an association of fundamental concepts in modeling, system analysis, estimation, optimization and optimal control. Our objectives are:
- To present an approach to make linear system identification algorithms more robust to noise in measurement data to accurately identify the dimension of the underlying dynamics.
- To develop a methodology to compute first order sensitivities of model dynamics with respect to physical parameters of the system while exploiting advances in linear system identification.
- To present a convex optimization based approach to identify nonlinearities involved in system dynamics from position and input time histories without any prior assumption on the structure of the system.
- To develop a general system identification framework for accurate but parsimonious representation of the system dynamics while integrating linear and nonlinear system identification techniques.
- To present means to adaptively refine the parameters of the mathematical representation of the system in real-time.
- To demonstrate the performance of the developed algorithms by considering real-engineering problems where traditional methods either fail or perform poorly.